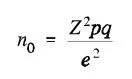HOW TO BUILD A PROFITABLE TRADING SYSTEM PART 1: CONFIDENCE IN NUMBERS
There is something very compelling about mathematics. There are no ‘buts’ and no ‘maybes’. Mathematics is not subjective. 2+2=4 and that's that – no matter how hard someone will try to insist that it is not. Numbers do not lie.
As an engineer, my love for numbers helped me in my trading from day one. I was never comfortable trading with subjective projections or on the recommendations of other traders. I needed concrete black-and-white proofs, with real hard numbers, to convince me that the trading rules and strategies I used had a statistical advantage and was profitable over time.
Any trading rules or strategies that I learned – whether from books, courses or other traders who came to me asking to automate their strategies – I rigorously tested to confirm their profitability. As you might have guessed, most of the trading strategies I tested over the last 14 years were shams, some even coming from prominent and highly respected traders. Out of almost a hundred different trading strategies that I tested, only a handful of them constantly made profits in the market.
While testing whether a strategy has worked in the past is a relatively simple task, the real challenge is evaluating its future profitability. Can we reasonably expect the strategy to perform the same in the future as it did in the past? Will we get the same results if we keep doing the same things we did 10 years ago? Most likely not since markets change all the time. To have the best shot of developing a trading strategy that not only worked in the past but also has a high chance of working in the future, we must employ the following three methods.
Statistical significance (Confidence in Numbers)
Continuous and automated strategy adjustments (when our knowledge changes our probabilities must change too)
CAN WE HAVE CONFIDENCE IN NUMBERS?
In this article, we will look at the first factor: statistical significance and what is required to have confidence in your numbers.
A widespread mistake by discretionary traders is to look only at small sample sizes (typically less than 100 trades) when building a strategy or deciding on a trading rule. Couple this with the human tendency to see what you want to see –and you can see how relying on manually performed subjective strategy tests can quickly go wrong. Performing tests manually often leads to errors and overconfidence in the test results. The only way to be confident in your statistics is if it’s performed in an automated way with a testing-algorithm applied to a large enough data set. What size sample is large enough? How to know if the results are due to pure luck or is statistically significant?
Don't worry; there is a formula for this.
It's called Cochran's Sample Size Formula.
Where:
Z is Z score
p is currently known result (for example 50% win rate for the strategy)
q is 1-p
e is margin of error (for example 5%)
With this formula, we can calculate how many trades we need to have in our sample size to be confident in the statistical result, given our margin of error. This test is commonly used with a 5% margin of error.
Putting some figures into the formula we get:
Confidence level 99%
(2.58)^2 (0.5)(0.5)/0.05^2 = 666
To be 99% confident with a projection that has a 5% margin of error we need 666 trades in our sample.
Confidence level 98%
(2.33)^2 (0.5)(0.5)/0.05^2 = 543
To be 98% confident with a projection that has a 5% margin of error we need 543 trades in our sample.
Confidence level 95%
(1.96)^2 (0.5)(0.5)/0.05^2 = 385
To be 95% confident with a projection that has a 5% margin of error we need 385 trades in our sample.
Confidence level 90%
(1.645)^2 (0.5)(0.5)/0.05^2 = 271
To be 90% confident with a projection that has a 5% margin of error we need 271 trades in our sample.
Confidence level 80%
(1.28)^2 (0.5)(0.5)/0.05^2 = 164
To be 80% confident with a projection that has a 5% margin of error we need 164 trades in our sample.
Confidence level 70%
(1.03)^2 (0.5)(0.5)/0.05^2 = 107
To be 70% confident with a projection that has a 5% margin of error we need 101 trades in our sample.
To be 70% confident in your statistical result, you need at least 107 trades in your test sample; to be 99% confidence you need 666 trades. A commonly accepted confidence level is 95%: thus when you have 385 trades in your test sample, you can be reasonably confident that the results are not obtained by chance.
WHAT IF YOU DON’T HAVE ENOUGH TRADES IN YOUR TEST SAMPLE?
If the signals of your trading strategy are rare and you don’t have the required sample size we’ve discussed, the best way to get more results is to combine test results from multiple markets. In particular, closely correlated markets. For example, you can expect the results for your strategy to be very similar on EURUSD and GBPUSD currency pairs since these currency pairs are closely correlated. But the important thing to remember is that the strategy rules must be exactly the same and you should not optimise the strategy separately for each market. The significance of this we cover in part two of this article series: How to build a profitable trading system Part 2: Antifragile trading systems.
Having a large enough sample size is very important when testing and developing trading strategies. If you’re using small sample sizes you risk picking up random noise obtained by chance alone. That’s not a good way to build your strategies. The larger the sample size the more confidence you can have in the statistical result.
More great posts: